import numpy as np
import jax
import jax.numpy as jnp
from jax import grad, jit
from jax.example_libraries import optimizers # for Adam optimizer
from scipy.optimize import minimize
import time
from functools import partial
import pandas as pd
import matplotlib.pyplot as plt
from typing import Tuple
from dataclasses import dataclass
# Set random seed for reproducibility
np.random.seed(42)
jax.config.update("jax_enable_x64", True)
@dataclass
class EarlyStoppingState:
"""State for early stopping and learning rate scheduling."""
best_sharpe: float = float('-inf')
patience_counter: int = 0
best_weights: jnp.ndarray = None
lr: float = 0.1
plateau_counter: int = 0
def generate_data(n_assets: int) -> Tuple[np.ndarray, np.ndarray]:
"""Generate random correlation matrix and expected returns."""
A = np.random.randn(n_assets, n_assets)
corr = A @ A.T
corr = corr / np.max(np.abs(corr))
returns = np.random.randn(n_assets) * 0.1 + 0.05
return corr, returns
# SciPy Implementation remains the same as before
def portfolio_stats_scipy(weights: np.ndarray,
corr: np.ndarray,
returns: np.ndarray,
risk_free_rate: float = 0.02) -> Tuple[float, float, float]:
port_return = np.sum(returns * weights)
port_vol = np.sqrt(weights.T @ corr @ weights)
sharpe = (port_return - risk_free_rate) / port_vol
return port_return, port_vol, sharpe
def negative_sharpe_scipy(weights: np.ndarray,
corr: np.ndarray,
returns: np.ndarray,
risk_free_rate: float = 0.02) -> float:
_, _, sharpe = portfolio_stats_scipy(weights, corr, returns, risk_free_rate)
return -sharpe
def optimize_scipy(corr: np.ndarray, returns: np.ndarray) -> Tuple[np.ndarray, float, float]:
n_assets = len(returns)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bounds = tuple((0, 1) for _ in range(n_assets))
start_time = time.time()
x0 = np.ones(n_assets) / n_assets
result = minimize(negative_sharpe_scipy, x0,
args=(corr, returns),
method='SLSQP',
bounds=bounds,
constraints=constraints)
end_time = time.time()
print('scipy optimization succeed:', result.success)
return result.x, -result.fun, end_time - start_time
# JAX Implementation with Adam
@jit
def portfolio_stats_jax(weights: jnp.ndarray,
corr: jnp.ndarray,
returns: jnp.ndarray,
risk_free_rate: float = 0.02) -> Tuple[float, float, float]:
port_return = jnp.sum(returns * weights)
port_vol = jnp.sqrt(weights.T @ corr @ weights)
sharpe = (port_return - risk_free_rate) / port_vol
return port_return, port_vol, sharpe
@jit
def negative_sharpe_jax(weights: jnp.ndarray,
corr: jnp.ndarray,
returns: jnp.ndarray,
risk_free_rate: float = 0.02) -> float:
_, _, sharpe = portfolio_stats_jax(weights, corr, returns, risk_free_rate)
return -sharpe
@jit
def projection_simplex(x: jnp.ndarray) -> jnp.ndarray:
"""Project onto probability simplex."""
x = jnp.clip(x, 0, None)
return x / jnp.sum(x)
def update_early_stopping_state(state: EarlyStoppingState,
current_sharpe: float,
current_weights: jnp.ndarray,
patience: int = 10,
min_improvement: float = 1e-4,
lr_reduction_factor: float = 0.5,
lr_patience: int = 5,
min_lr: float = 1e-6) -> EarlyStoppingState:
if current_sharpe > state.best_sharpe + min_improvement:
state.best_sharpe = current_sharpe
state.best_weights = current_weights
state.patience_counter = 0
state.plateau_counter = 0
else:
state.patience_counter += 1
state.plateau_counter += 1
if state.plateau_counter >= lr_patience and state.lr > min_lr:
state.lr *= lr_reduction_factor
state.lr = max(state.lr, min_lr)
state.plateau_counter = 0
print(f"Reducing learning rate to {state.lr}")
return state
def optimize_jax(corr: np.ndarray,
returns: np.ndarray,
n_iterations: int = 1000,
initial_lr: float = 0.01, # Lower initial learning rate for Adam
patience: int = 10,
min_improvement: float = 1e-4,
lr_patience: int = 5,
lr_reduction_factor: float = 0.5,
min_lr: float = 1e-6,
b1: float = 0.9, # Adam beta1
b2: float = 0.999, # Adam beta2
eps: float = 1e-8 # Adam epsilon
) -> Tuple[np.ndarray, float, float]:
"""Optimize portfolio using JAX with Adam optimizer."""
# Convert inputs to JAX arrays
corr = jnp.array(corr)
returns = jnp.array(returns)
# Initialize weights and early stopping state
n_assets = len(returns)
init_weights = jnp.ones(n_assets) / n_assets
state = EarlyStoppingState(lr=initial_lr, best_weights=init_weights)
start_time = time.time()
# Initialize Adam optimizer
opt_init, opt_update, get_params = optimizers.adam(
step_size=state.lr,
b1=b1,
b2=b2,
eps=eps
)
opt_state = opt_init(init_weights)
# Gradient function
grad_sharpe = jit(grad(negative_sharpe_jax))
# Optimization loop
for iteration in range(n_iterations):
weights = get_params(opt_state)
weights = projection_simplex(weights) # Project to satisfy constraints
gradient = grad_sharpe(weights, corr, returns)
opt_state = opt_update(iteration, gradient, opt_state)
current_sharpe = -negative_sharpe_jax(weights, corr, returns)
# Update early stopping state
state = update_early_stopping_state(
state,
current_sharpe,
weights,
patience=patience,
min_improvement=min_improvement,
lr_patience=lr_patience,
lr_reduction_factor=lr_reduction_factor,
min_lr=min_lr
)
# Check early stopping condition
if state.patience_counter >= patience:
print(f"Early stopping triggered at iteration {iteration}")
break
end_time = time.time()
final_sharpe = state.best_sharpe
return np.array(state.best_weights), float(final_sharpe), end_time - start_time
def compare_optimizers() -> pd.DataFrame:
"""Compare JAX and SciPy optimizers using logspaced number of assets."""
# Create logspaced array of asset numbers from 5 to 500 with 10 points
asset_numbers = np.unique(np.logspace(np.log10(5), np.log10(500), 10).astype(int))
results = []
for n_assets in asset_numbers:
print(f"Processing {n_assets} assets...")
corr, returns = generate_data(n_assets)
# Run SciPy optimization
scipy_weights, scipy_sharpe, scipy_time = optimize_scipy(corr, returns)
# Run JAX optimization with Adam
jax_weights, jax_sharpe, jax_time = optimize_jax(
corr,
returns,
n_iterations=1000,
initial_lr=0.01,
patience=10,
min_improvement=1e-4,
lr_patience=5,
lr_reduction_factor=0.5,
min_lr=1e-6
)
results.append({
'n_assets': n_assets,
'scipy_time': scipy_time,
'jax_time': jax_time,
'scipy_sharpe': scipy_sharpe,
'jax_sharpe': jax_sharpe
})
return pd.DataFrame(results)
# Run comparison
results_df = compare_optimizers()
# Create visualization
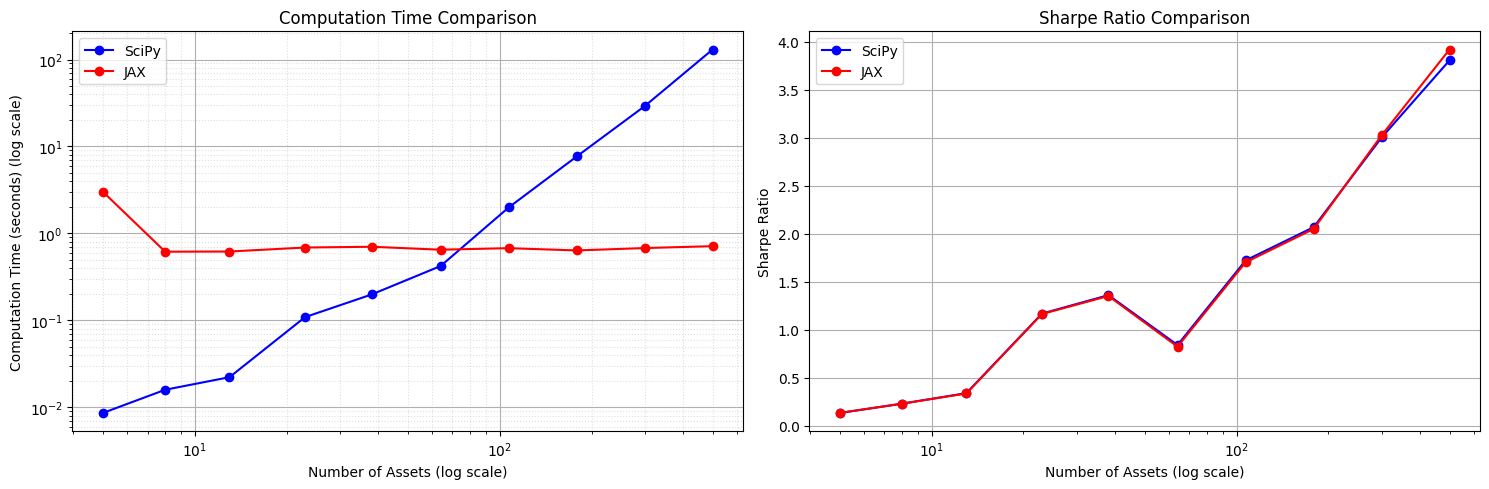
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
# Plot computation time comparison with log scale
ax1.loglog(results_df['n_assets'], results_df['scipy_time'], 'b-o', label='SciPy')
ax1.loglog(results_df['n_assets'], results_df['jax_time'], 'r-o', label='JAX')
ax1.set_xlabel('Number of Assets (log scale)')
ax1.set_ylabel('Computation Time (seconds) (log scale)')
ax1.set_title('Computation Time Comparison')
ax1.legend()
ax1.grid(True, which="both", ls="-")
ax1.grid(True, which="minor", ls=":", alpha=0.4)
# Plot Sharpe ratio comparison with log scale
ax2.semilogx(results_df['n_assets'], results_df['scipy_sharpe'], 'b-o', label='SciPy')
ax2.semilogx(results_df['n_assets'], results_df['jax_sharpe'], 'r-o', label='JAX')
ax2.set_xlabel('Number of Assets (log scale)')
ax2.set_ylabel('Sharpe Ratio')
ax2.set_title('Sharpe Ratio Comparison')
ax2.legend()
ax2.grid(True)
plt.tight_layout()
print("Results DataFrame:")
print(results_df)
print("\nAsset numbers tested:", sorted(results_df['n_assets'].unique()))